« Une histoire de l'évapotranspiration » : différence entre les versions
m (TOC) |
m (Correction erratas (morceau de phrase dupliquée, etc.)) |
||
| Ligne 9 : | Ligne 9 : | ||
|Allemand= | |Allemand= | ||
|Espagnol= | |Espagnol= | ||
|Complément 1= | |Complément 1= | ||
|Annexe 1=Remarques sur l’eau de la pluie, & sur l’origine des Fontaines… (La Hire, [1703] 1720). | |Annexe 1=Remarques sur l’eau de la pluie, & sur l’origine des Fontaines… (La Hire, [1703] 1720). | ||
|Annexe 2=Le dispositif de Guettard (1748) pour mesurer la transpiration d’un organe végétal. | |Annexe 2=Le dispositif de Guettard (1748) pour mesurer la transpiration d’un organe végétal. | ||
| Ligne 114 : | Ligne 114 : | ||
===Transpiration végétale=== | ===Transpiration végétale=== | ||
La circulation de la [[sève]] (eau + « sucs » nourriciers dissous) des racines jusqu’aux feuilles où elle s’évapore, était connue au Moyen-âge (Crescens, [''ca.'' 1306] 1373, livre II) ; et le lien entre transpiration et absorption racinaire (« suction ») établi au milieu du XVIII<sup>e</sup> | La circulation de la [[sève]] (eau + « sucs » nourriciers dissous) des racines jusqu’aux feuilles où elle s’évapore, était connue au Moyen-âge (Crescens, [''ca.'' 1306] 1373, livre II) ; et le lien entre transpiration et [[absorption racinaire]] (« suction ») établi au milieu du XVIII<sup>e</sup> siècle : d’un côté, pour qu’il y ait transpiration, il faut que les racines puissent fournir assez d’eau pour remplacer celle qui s’évapore ; de l’autre, tout ce qui réduit ou arrête la transpiration réduit ou arrête la « suction » et donc la [[nutrition]] de la plante. | ||
Le lien entre transpiration, respiration et échanges gazeux de la photosynthèse qui, passant par les stomates, sont réduits ou arrêtés par la [[régulation stomatique]], s’est fait progressivement, de la fin du XVIII<sup>e</sup> siècle à celle du XIX<sup>e</sup>. | Le lien entre transpiration, respiration et échanges gazeux de la photosynthèse qui, passant par les stomates, sont réduits ou arrêtés par la [[régulation stomatique]], s’est fait progressivement, de la fin du XVIII<sup>e</sup> siècle à celle du XIX<sup>e</sup>. | ||
| Ligne 216 : | Ligne 216 : | ||
La même année mais de façon indépendante, Penman propose, sur la base d’un bilan d’énergie et de transfert de vapeur, une première formulation théorique, qui fut précisée en 1965 par Monteith (formule de Penman-Monteith<ref>Voir [https://en.wikipedia.org/wiki/Penman%E2%80%93Monteith_equation article de Wikipedia] ou [http://www.fao.org/docrep/X0490E/x0490e06.htm#formulation%20of%20the%20penman%20monteith%20equation exposé] sur le site de la FAO.)</ref>) et s’est imposée dans le monde comme la référence pour estimer l’ETP ('''voir article [[Évapotranspiration]]'''). | La même année mais de façon indépendante, Penman propose, sur la base d’un bilan d’énergie et de transfert de vapeur, une première formulation théorique, qui fut précisée en 1965 par Monteith (formule de Penman-Monteith<ref>Voir [https://en.wikipedia.org/wiki/Penman%E2%80%93Monteith_equation article de Wikipedia] ou [http://www.fao.org/docrep/X0490E/x0490e06.htm#formulation%20of%20the%20penman%20monteith%20equation exposé] sur le site de la FAO.)</ref>) et s’est imposée dans le monde comme la référence pour estimer l’ETP ('''voir article [[Évapotranspiration]]'''). | ||
Ironie de l’histoire, Penman | Ironie de l’histoire, Penman calibre cette formule en exploitant les données obtenues sur un dispositif expérimental (des lysimètres de 6 pieds de profondeur, contenant les uns de l’eau, d’autres du sol resté nu et d’autres du sol avec du [[gazon]]) dont la conception de base était proche de celui installé par La Hire en 1688… Il exprime l’évapotranspiration du gazon et l’évaporation du sol nu comme des fractions de l’évaporation de l’eau libre. | ||
Pendant longtemps, l’usage de la formule de Penman-Monteith fut restreint à ceux qui disposaient de moyens de calculs puissants et aux rares stations météo où les nombreuses données qu’elle exige étaient mesurées, d’où la création d’autres formules - aussi diverses que nombreuses - moins sûres mais d’emploi plus facile. L’avènement de la micro-informatique et des stations météo automatiques en permet maintenant une utilisation beaucoup plus large, rendant les autres sans intérêt. | Pendant longtemps, l’usage de la formule de Penman-Monteith fut restreint à ceux qui disposaient de moyens de calculs puissants et aux rares stations météo où les nombreuses données qu’elle exige étaient mesurées, d’où la création d’autres formules - aussi diverses que nombreuses - moins sûres mais d’emploi plus facile. L’avènement de la micro-informatique et des stations météo automatiques en permet maintenant une utilisation beaucoup plus large, rendant les autres sans intérêt. | ||
Version du 19 décembre 2024 à 10:19
| La circulation d’eau dans les plantes est un sujet vaste et complexe, qui sera traité en plusieurs articles. Celui-ci est une lecture particulière de 4 siècles d’histoire (1674-1961). |
Auteur : Pierre Morlon
| Le point de vue de... | |
|---|---|
Pas de compléments pour cet article
| |
| Annexes de l'article | |
| Voir aussi (articles complémentaires) | |
| Autres langues | |
| Informations complémentaires | |
Article accepté le 1er mars 2017
| |
| Article mis en ligne le 1er mars 2017 |
| « « … tout se réduira donc à considérer la dépense que les végétaux font de la pluie, comme une espèce d’évaporation, puisque tout ce qui entre dans la circulation est fourni par les racines. Ainsi l’on doit entendre que les végétaux tirent de la terre plus ou moins humide, par leurs racines, de l’eau qui s’évapore le jour par les pores des feuilles. Cette dépense est considérable, mais il ne faut pas en abuser pour conclure l’insuffisance des pluies ; car quand un terrain est recouvert de plantes, il ne s’évapore que très-peu d’eau immédiatement du fond de la terre ; tout s’opère par les végétaux : d’ailleurs cette évaporation ne dure qu’une petite partie de l’année » » (Desmarest, 1757 : 89.). |
Introduction.
« La compréhension des mécanismes du transport de l’eau du sol à l’atmosphère à travers l’arbre [ou plus généralement toute plante] est à la fois un des problèmes (…) les plus anciennement étudiés et l’un de ceux qui a suscité le plus de polémiques et qui a le plus résisté aux investigations » (Cruiziat, 2007). Cet article tente d’expliquer un paradoxe.
D’un côté, l’évaporation de l’eau par, ou à travers, les (couverts) végétaux est une observation aussi ancienne que l’agriculture. Citons seulement un passage du livre d’Isaïe dans la Bible (500 av. J.-C.) : « Oui, comme la pluie et la neige tombent des ciels et n’y retournent pas sans avoir désaltéré la terre, sans l’avoir fait enfanter et germer (…) » (traduction Chouraqui, 2003).
De l’autre, bien qu’on ait compris dès le XVIIIe siècle le lien entre la transpiration des végétaux et la « suction » (l’absorption par les racines des « sucs nourriciers » alors non identifiés), ce n’est que bien avancé le XXe siècle – après l’alimentation minérale, la photosynthèse, la respiration, la fixation symbiotique, l’hérédité – que ses mécanismes ont pu être compris et quantifiés (« modélisés ») à partir de données facilement mesurées.
Le sujet est certes difficile et complexe. « Il est très difficile de faire ces expériences d’une manière un peu constante, parce que l’état de la plante, de l'eau, & l'action du soleil varient beaucoup. (…) Il est assez difficile d'estimer la transpiration, parce qu'il est très difficile de pouvoir tenir compte de tout ce qui influe sur elle » (Sénebier, 1791, article TRANSPIRATION : 284 & 285).
Et comment relier entre elles des observations portant sur les mêmes phénomènes mais faites à des échelles très différentes pour répondre à des questions différentes (tableau 1) : le bassin versant d’un cours d’eau (quelle proportion des pluies alimente les sources et rivières ?) ; le champ cultivé (quand irriguer et combien ?) ; la plante isolée, le rameau ou la feuille (comment fonctionnent les plantes ? Le font-elles toutes de la même façon ?) ; le stomate ou le vaisseau (id.) ? « Ce qui manque le plus pour dégager cette science nouvelle qu'est l'hydrométéorologie de ses tâtonnements de début, c'est, à notre avis, la coordination des études et des méthodes de recherches », constatent Coutagne & de Martonne en 1933.
| Méthode | Échelle espace | Échelle temps | XVIIe s. | XVIIIe s. | XIXe s. | XXe s. |
| Déficit d’écoulement de cours d’eau (pluies estimées moins eau écoulée) | > 103 km2 | an | Perrault | Coutagne & de Martonne (1933), Hénin et al. (1944), Turc (1951, 1954) | ||
| Champ cultivé (pluie + irrigation – drainage) | > 102 à 104 m2 | mois | Risler | Thornthwaite | ||
| Lysimètre à drainage (pluie + irrigation – drainage) | dm2 à m2 | mois à jour | La Hire | Thornthwaite, Penman[1], Turc (1955, 1961), Bouchet | ||
| Plante entière ou organe (perte d’eau) | dm2 | jour à heure | Mariotte, Woodward | Hales, Miller, Sénebier | Saussure, Risler | |
| Organe végétal (eau condensée) | cm2 | jour à heure | Hales, Guettard, Duhamel, Sénebier | Saussure, Dehérain, Risler |
Tout cela a joué. Mais notre thèse ici est qu’une idée fausse, énoncée au départ comme une hypothèse parmi d’autres mais vite implicitement admise sans discuter, a empêché des savants parmi les plus grands de tirer les conclusions que leurs observations suggéraient, et les a conduits à préférer des chiffres en apparence précis, mais entachés de (très) gros biais non maîtrisés, à des chiffres non biaisés mais moins précis. D’où deux siècles de piétinements, voire de reculs.
Quelques repères chronologiques aideront à caler cette histoire.
Quelques repères chronologiques.
Évaporation de l’eau dans l’air.
L’action du soleil, de la chaleur et du vent sur l’évaporation de l’eau, qu’elle soit libre ou contenue dans la terre humide, est une observation immémoriale.
En physique, c’est à l’aube du XIXe siècle que les lois de l’évaporation sont établies :
Elle consomme beaucoup d’énergie et refroidit donc la surface où elle se produit. Sa chaleur latente (restituée lorsque la vapeur se condense) est proche de 600 calories par gramme d’eau évaporée. La calorie étant définie comme la quantité de chaleur mise en jeu dans une variation de température de 1°C d’un gramme d’eau, cela veut dire, par exemple, que l’évaporation d’un seul gramme d’eau refroidit de 10°C une masse de 60 g d’eau.
D’autre part, elle ne peut se faire que si l’air n’est pas saturé d’humidité. Sa vitesse dépend du déficit de saturation de l’air, qui est la différence entre la pression de vapeur saturante à la température de cet air et la pression partielle de la vapeur d’eau qu’il contient (l’humidité relative étant, elle, le rapport entre ces deux grandeurs). Plus l’air est chaud, plus il peut contenir de vapeur d’eau : dans la gamme de températures où poussent les végétaux, la pression de vapeur saturante double tous les 10 à 12°C (Dalton, 1802). Ce que Boussingault (1844 : 691) et Gasparin (1860 : 65-66) exposent dans leurs ouvrages d’agriculture.
Découlant de la physique, l’idée d’un maximum climatique possible d’évaporation pour une surface d’eau libre (en allemand klimatischen Evaporationskraft, Mühry, 1860 ; Vivenot, 1866) apparaît au milieu du XIXe siècle.
Transpiration végétale
La circulation de la sève (eau + « sucs » nourriciers dissous) des racines jusqu’aux feuilles où elle s’évapore, était connue au Moyen-âge (Crescens, [ca. 1306] 1373, livre II) ; et le lien entre transpiration et absorption racinaire (« suction ») établi au milieu du XVIIIe siècle : d’un côté, pour qu’il y ait transpiration, il faut que les racines puissent fournir assez d’eau pour remplacer celle qui s’évapore ; de l’autre, tout ce qui réduit ou arrête la transpiration réduit ou arrête la « suction » et donc la nutrition de la plante. Le lien entre transpiration, respiration et échanges gazeux de la photosynthèse qui, passant par les stomates, sont réduits ou arrêtés par la régulation stomatique, s’est fait progressivement, de la fin du XVIIIe siècle à celle du XIXe.
Des débuts prometteurs, puis on piétine… ou recule.
A la fin du XVIIe siècle, Pierre Perrault, le frère de l’auteur des Contes, estime le débit de la Seine à 3 lieues de sa source et la pluie tombée pendant un an sur son bassin. En unités actuelles, cela donne 485 mm de pluie, 78 mm d’écoulement de la Seine, soit un déficit d’écoulement apparent (« déchet ») de 407 mm, qui est une estimation de ce que nous appelons évapotranspiration réelle. Estimation qu’il reconnaît très grossière : « Je sais bien que cette déduction n’a aucune sûreté : mais qui pourrait en donner une qui fût certaine ? » (1674 : 200-205)… mais qui n’est pas très éloignée de celles faites actuellement !
Son contemporain La Hire mesure la pluviométrie annuelle à Paris, et installe en 1688 ce qu’on appelle maintenant un lysimètre à drainage, de 4 pieds de superficie (0,169 m2) et de 8 pieds (2,6 m) de profondeur, avec des rebords pour éviter le ruissellement, et entouré par ce que nous appelons un anneau de garde. Il met au fond des cailloux pour éviter que le tuyau de sortie ne se bouche, puis remplit d’une terre perméable ([1703] 1720 : 57-61) (Annexe 1).
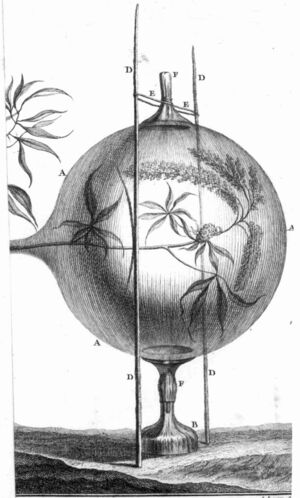
Dans les années 1720, Hales calcule que « l’évaporation de la surface de l’eau est à l’évaporation de la surface de la terre [nue], comme 10 sont à 3[2] » ([1727] 1735 : 48). Avec un dispositif (fig. 1, voir annexe 3) pesé matin et soir dans différentes conditions météorologiques, il mesure la transpiration d’un pied de tournesol et la rapporte à la surface totale des feuilles de la plante ainsi qu’à celle des racines ; dans une autre expérience, il calcule en pouces la hauteur d’eau transpirée sur un arpent de houblon (id : 3ss ; 27-28). En 1726 Miller établit que la quantité d’eau évaporée est en général proportionnelle à la température du jour ; Guettard en 1748-49 (fig. 2 et annexe 2) sépare l’action du rayonnement solaire de celle de la température et affirme le rôle du renouvellement de l’air…
En 1758, Duhamel du Monceau conclut de leurs expériences « La différente température de l’air influe beaucoup sur la transpiration ; le froid, l’humidité la diminuent ou la suppriment entièrement (…) la transpiration des plantes est peu considérable dans les temps de pluie, & même quand le ciel est couvert de nuages ; & elle n’est jamais plus abondante que quand le soleil est net & ardent, & encore lorsqu’il fait du vent & du hâle, pourvu toutefois que la terre ne soit pas extrêmement sèche, & que les racines en puissent pomper toute la sève dont la plante a besoin » (p. 141 & 148) – ce qui ne répond pas à toutes les questions posées alors, ni n’empêche d’autres conclusions qui, plus tard, se révélèrent erronées.
Mais ensuite, on piétine. En physiologie, Dehérain (1873) se pose les mêmes questions que Guettard en 1748-48 et, pour y répondre, emploie un dispositif expérimental similaire (fig. C) ; en hydrologie, on n’a que bien peu avancé entre l’estimation de Perrault en 1674 et la synthèse de Coutagne et de Martonne en 1933.
Ayant établi mois par mois le bilan hydrique d’une pièce de terre de 1,23 ha, dont il s’est assuré qu’elle est hydrauliquement isolée et que « toute l'eau qui n'est pas évaporée est recueillie par les drains », Risler (1869, 1870, 1871) (voir annexe 5) n’utilise ces données que pour borner les résultats de mesures sur organes végétaux, compte tenu des très gros biais qui doivent entacher ces dernières ! Pourquoi ? Il explique à la fin : « Dans les deux Mémoires que j’ai déjà publiés sur l’évaporation du sol, j’avais cherché à déterminer cette évaporation par la différence entre la quantité de pluie tombée sur une certaine surface et la quantité d’eau écoulée par les drains. Mais cette différence comprend à la fois l’eau évaporée directement par le sol et l’eau évaporée ou transpirée par l’intermédiaire des plantes ».
Séparer à tout prix, fût-ce celui de biais expérimentaux non contrôlés, la transpiration des plantes de l’évaporation du sol, n’a de sens que si l’on pense que transpiration végétale et évaporation de l’eau libre ne sont pas de même nature. Or, même lorsqu’elle n’est pas explicite, l’idée que les plantes ont un rôle actif dans la transpiration est, jusque très tard, sous-jacente à une grande partie de la littérature. Par des mécanismes - éventuellement différents selon les espèces, d’où la multiplication des mêmes expériences sur des plantes différentes - que les physiologistes ont passé beaucoup de temps à vouloir découvrir, la transpiration des plantes était ainsi supposée pouvoir être supérieure à l’évaporation d’une surface d’eau libre dans les mêmes conditions.
A une époque où les savants avaient pourtant une vue plus large des choses que les chercheurs de maintenant, seule cette conviction peut expliquer que, étudiant la transpiration des végétaux, certains d’entre eux ne tiennent pas compte des connaissances en physique de leur époque[3] . D’où : pas de calcul d’un bilan d’énergie ; pas de limitation par l’énergie disponible, proportionnelle à la surface du terrain et non des organes végétaux, car fournie par le rayonnement solaire et redistribuée par divers mécanismes dont les mouvements de l’air. C’est elle qui conduisait à rapporter la quantité d’eau transpirée, non à la surface du terrain comme on le fait maintenant (ou comme Hales l’avait fait dès 1727), mais à la surface foliaire ou, celle-ci étant difficile à évaluer, au poids vert…
Des théories sur la transpiration des plantes.
Toute observation est guidée par la théorie que l’on a. Comment expliquer que l’eau monte des racines aux feuilles dans le sens contraire de celui qu’impose la gravité ? Et que, dans les arbres, elle monte plus haut que les 10 mètres équilibrés par la pression atmosphérique ? Deux types d’explications sont avancées.
Explications physiques.
Elles furent très diverses. Voici deux exemples tirés d’une vaste littérature :
« Il n’y a pas tant de difficulté à expliquer comment les sucs de la terre entrent dans la racine des Plantes. La pluie, ou l’eau des arrosements détrempe les sels de la terre : voilà les sucs en mouvement. Il ne faut plus que la chaleur souterraine, pour les pousser en haut ; après cela survient la chaleur du Soleil qui dilate les pores de la Plante, & qui ouvre un passage aux sucs, pour s’élever dans la tige, & dans les branches. (…) Voilà donc notre Acteur trouvé, pour faire entrer les sucs nourriciers dans les racines des Plantes : le feu souterrain pousse ces sucs jusqu’à la tige ; alors la chaleur du Soleil survient, qui fait le reste, en les élevant jusqu’aux extrémités des branches : peut-être parce qu’il dilate leurs pores & leurs fibres ; ou bien parce qu’il subtilise la matière des sucs, en les réduisant en vapeurs & en fumées ; ou plutôt parce qu’il fait tous les deux à la fois. » (Vallemont, 1705 : 105-106 & 116-117).
« La première question qui se présente ici, c’est comment ces sucs montent au haut des plantes & des arbres (…) La raison qu'on en donne ordinairement, c’est à dire l'action des vaisseaux capillaires, me paraît très suffisante. (…) Une autre force qui contribue beaucoup à élever la sève, c’est l'attraction naturelle entre les parties constitutives de ce fluide. (…) Ces deux causes agissant ensemble, & l'évaporation se faisant continuellement par les parties supérieures des vaisseaux, la sève s'élève des racines des plantes jusqu'aux extrémités de leurs branches. » (Home, [1757] 1761 : 129-130).
Explications vitalistes.
| « Les plantes transpirent, poussent au-dehors la matière de la transpiration, & elle s’évapore [...] La plante, après s’être approprié les principes qu’elle reçoit de l’atmosphère, lui renvoie le surplus pour y éprouver de nouvelles décompositions & de nouvelles recombinaisons ; la végétation reçoit la vie par cette circulation générale… » (Rozier, 1783, 408.). |
Les explications « vitalistes », postulent un rôle actif de la plante, par analogie entre plantes et animaux, suite à la publication de la circulation du sang par Harvey en 1628. Bien que dès 1727 Hales ait démontré que, dans les plantes, la sève ne circule pas dans un circuit fermé sous pression, ces analogies ont joué un grand rôle. « Ayant ici donné le rapport du poids, de la grosseur, grandeur & surface de cette plante, & des quantités qu’elle tire & transpire, ne conviendrait-il pas à présent d’en faire la comparaison avec la nourriture & la transpiration du corps humain ? (…) Ainsi la transpiration d’un homme est à celle d’un Soleil ((tournesol)), comme 141 sont à 100. » (Hales [1727] 1735 : 7ss ; voir en annexe 3 un résumé de la suite par Duhamel du Monceau).
Les animaux secrétant de l’urine et excrétant des déjections, il fallait bien que les plantes fassent de même. La transpiration fut ainsi vue :
- - soit comme un moyen d’évacuer l’eau supposée « en excès » dans la plante - une idée aussi fausse qu’ancienne[4]. mais qui a la vie dure : « TRANSPIRATION. Biol. vég. Rejet de vapeur d'eau dans l'atmosphère de l'excès d'eau amené par la sève brute » (Habault, 1983 : 140) ; « Transpiration végétale. Émission dans l'atmosphère, sous forme de vapeur d'eau, de l'excès d'eau amené par la sève brute » (Trésor de la Langue Française, consulté le 26 décembre 2016).
- - soit comme une sécrétion qui épure la sève en éliminant des déchets (excréments), et on nomma glandes les stomates observés au microscope comme des points lumineux.
« D’où on conclut qu’elles [les feuilles] sont des organes destinés à opérer une sécrétion très-importante à l’économie végétale », écrit Duhamel du Monceau (1750, Préface, viii) qui parle de la transpiration comme « dépuration de la sève » (id. : 15) et affirme plus tard « Les feuilles sont donc des organes sécrétoires, par lesquels les arbres se déchargent d’un suc trop abondant ou inutile. (…) On sait qu’indépendamment des gros excréments dont les animaux se déchargent, leurs liqueurs se dépurent encore, & fournissent d’autres évacuations connues sous les noms de transpiration sensible, & transpiration insensible. (…) Cette prodigieuse transpiration est d’autant plus nécessaire que les plantes n’ont que cette seule voie pour se décharger de ce qui devient inutile pour leur nourriture : il était donc nécessaire que les feuilles eussent de grandes surfaces pour suffire à cette sécrétion; au lieu que l’homme, outre cette faculté de transpirer, a encore l’évacuation des gros excréments, des urines, de la salive, de ce qui s’échappe par les narines, par la respiration, etc. » (1758 : 133-134 & 139, voir annexe 3).
Bien qu’ayant montré qu’on peut reproduire expérimentalement les caractéristiques de la montée de la sève et de la transpiration sur des feuilles artificielles de toile, donc par des forces purement physiques, Sénebier (1791, article TRANSPIRATION : 283, voir annexe 4) écrit dans le même ouvrage : « Mais quand on réfléchit à la force d'ascension des pleurs de la vigne, quand on pense que les tiges mortes avec leurs feuilles ne sucent presque point d'eau, il faut reconnaître qu'il doit y avoir plus qu'une impulsion purement mécanique pour donner le branle à la végétation et pour l’entretenir. » (article ANALOGIE ENTRE LES PLANTES ET LES ANIMAUX : 11).
Conséquences méthodologiques : à quelles échelles, avec quelles extrapolations… et quels biais ?
On a ici un exemple de comment la représentation que l’on a d’un phénomène - la théorie - détermine la façon d’observer ce phénomène, et en retour comment les observations ainsi faites empêchent l’éclosion d’une autre théorie.
Si la transpiration est passive, physique - rien que de l’évaporation - il est logique de la rapporter à l’énergie reçue, proportionnelle à la surface du terrain car d’origine solaire.
Si par contre elle est active, il est logique de la rapporter à la surface des organes transpirants, les feuilles, et on peut le faire dans des conditions pouvant être très éloignées des naturelles. Mais cette surface étant difficile à estimer avec précision, on l’a vite remplacée par leur poids. Hales avait rapporté l’eau évaporée à la surface des feuilles, et Guettard affirmé que « deux parties semblables d'une même plante transpirent en raison de leur surface ». Mais, pendant 150 ans, préférant la précision apparente de la mesure du poids à l’imprécision de celle de la surface, on rapporta l’eau transpirée au poids de la plante ou de l’organe : plus on a voulu contrôler, moins les mesures ont signifié quelque chose !
Or toute quantification pose la question de l’extrapolation à d’autres échelles que celle à laquelle on a fait les mesures. Tous les dispositifs n’étaient pas adaptés pour mesurer, sans biais et de façon généralisable et extrapolable, l’influence des différents facteurs. « Ces méthodes sont très artificielles, et la généralisation à partir d’elles donne parfois des résultats impossibles. Par exemple, dans une étude, la transpiration d’une forêt de chênes a été calculée comme étant plus de huit fois le total des pluies », constate Thornthwaite en 1948.
L’extrapolation au couvert végétal se fit en multipliant la transpiration par unité de poids du végétal par la masse de la végétation par unité de surface de terrain, avec des résultats hasardeux. Au milieu du XIXe siècle, Gasparin fait le calcul suivant : « Quelle est cette quantité d’eau suffisante pour fournir à l’évaporation des plantes ? Avant et pendant sa floraison, la luzerne évapore en 24 heures 112,94 g d’eau par kg de son poids à l’état vert, ce qui revient à 451,76 g par kg de son poids à l’état sec. On obtient d’un hectare de luzerne, du 1er au 30 juin, une repousse donnant une coupe de 2 000 kg de fourrage sec. Pendant la durée de sa croissance, elle avait donc un poids moyen de 1 000 kg de fourrage équivalant à 4 000 kg à l’état vert ou 0,4 kg par m2 de surface de sol. Il y aura donc, pour chaque jour, une évaporation moyenne de 45,18 g d’eau par m2, et pour le mois de juin entier 1355,4g. Pendant ce même mois de juin 1852 (…), une surface aqueuse a évaporé 130,8 kg par m2, l’évaporation de la luzerne est donc d’environ 1,04/100 de l’évaporation de l’eau » (1860 : 67). Même en l’absence d’irrigation, la valeur de la transpiration, 1,35 mm pour un mois de juin (sec, selon la note de bas de page) est aberrante !
Lorsque, avec le même genre d’extrapolation, Dehérain (1873 : 184) aboutit à 3 mm pour une journée claire de juillet près de Paris, une valeur vraisemblable, est-ce parce que les biais de sens contraire se sont compensés ? Ce qu’évoque Risler en 1871 : « On pourrait croire que la transpiration est beaucoup plus grande dans ces tubes ou flacons qu’à l’air libre. Mais on verra, en comparant les résultats de cette méthode à ceux des premières, que cela n’est pas. Si la chaleur est plus forte dans les tubes qu’à l’air extérieur, elle tend à accroître la transpiration, mais la vapeur d’eau y est également plus abondante et tend à la diminuer. (…) Une bonne précaution à prendre lorsqu’on emploie les tubes ou flacons, c’est de ne pas les exposer à un soleil ardent avant qu’il s’y soit dégagé une certaine quantité de vapeur qui, en se condensant sur leurs parois, forme une sorte d’écran ». C’est ainsi qu’il arrive à un résultat surprenant : « Je n'ai pu constater aucune variation de la transpiration avec l'humidité ou avec l'agitation de l'air. Si ces rapports existent, comme on l'a affirmé, ils sont ordinairement effacés par les autres »…
Outre leur poids, Risler (1871) mesure la surface des feuilles et calcule l’eau transpirée pour 100 cm2 de cette surface. « Pour passer de là à la transpiration moyenne par hectare, il fallait déterminer la surface des feuilles qui couvrent un hectare ou du moins un mètre carré. J’ai fait un certain nombre de ces déterminations » Mais il fait remarquer que « dans un champ de blé, de maïs-fourrage et de trèfle très épais, comme dans une forêt touffue, les feuilles supérieures font ombre aux feuilles inférieures, et par conséquent diminuent leur transpiration ».
La sortie du tunnel.
Nous n’évoquerons ici que quelques points.
Dixon, 1914 : la transpiration et la montée de la sève.
C’est en 1914 que Dixon donne de la transpiration et de la montée de la sève contre la gravité l’explication purement physique actuellement bien vérifiée, liée à la courbure des surfaces d’évaporation et à la pression négative dans les vaisseaux de sève (Cruiziat, 2007). L’eau s’évapore de la paroi des cellules sous-stomatiques et dans les aérenchymes. L’eau liquide se replie alors dans des pores de plus en plus fins (jusqu’à l’ordre du nanomètre) au sein des parois, ce qui engendre des ménisques et des tensions de plusieurs dizaines de bars, bien supérieures à la pression atmosphérique, ce qui explique que l’eau puisse monter à plus de 10 mètres de haut dans des arbres. La cohésion de l’eau liquide transmet ces tensions aux colonnes d’eau circulant dans les vaisseaux qui se mettent donc sous tension, provoquant le mouvement dans le système vasculaire de la plante. A l’extrémité de ce réseau, il s’instaure donc entre l’eau du sol et celle des racines une différence de potentiel hydrique qui entretient le flux transpiratoire. Dans les plantes, l’eau se déplace sous la seule action des forces physiques.
Mais, en Europe, 1914 n’était pas le meilleur moment pour diffuser une théorie de physiologie végétale : l’idée d’un rôle actif des plantes, donc d’une transpiration pouvant être supérieure à l’évaporation d’une surface d’eau libre, perdura…
Deux obstacles.
Des évaporations dépassant celle d’une surface d’eau libre ?
Et il n’y avait pas que la transpiration qui fût supposée pouvoir être supérieure à l’évaporation de l’eau libre ; on a imaginé que ce pouvait aussi être le cas de l’évaporation depuis la surface du sol. En 1933 encore, Coutagne et de Martonne définissent l’« évaporation hydrologique » : « la dissipation de l'eau des précipitations, d'où résulte le déficit d'écoulement, est due avant tout à un processus qui n'est pas identique à l'évaporation physique définie plus haut. Ce n'est pas généralement une nappe d'eau qui évapore, c'est le sol, plus ou moins humide en surface et en profondeur. Il s'agit d'une évaporation physique de caractère spécial, à laquelle s'ajoute l'évaporation physiologique de la végétation. Cette « évaporation hydrologique » (…) est généralement inférieure à l'évaporation physique, pour différentes raisons », mais « il n'est pas impossible que l'évaporation hydrologique atteigne ou dépasse l'évaporation physique pendant une partie de l'année. (…) il n'est pas impossible que l'évaporation hydrologique de la saison chaude atteigne ou dépasse l'évaporation physique (d'autant plus que l'évaporation physiologique s'y ajoute) ».
Une voie sans issue : l’évaporation, fonction directe de la pluie.
Sans doute parce que sa question de départ porte plus sur l’alimentation des sources et rivières que sur les besoins en eau des cultures, Risler applique, pour un champ cultivé, l’idée d’un maximum possible non à la valeur absolue de l’évaporation, mais au pourcentage d’eau de pluie qui s’est évaporé – d’abord à l’échelle annuelle puis, ayant mesuré l’humidité du sol à la fin de chaque mois, mensuelle.
A partir du bilan de bassins versants de rivières, à l’échelle annuelle, c’est encore en fonction de la pluie que Hénin & Ternissien (1944) construisent une formule de l’évaporation mathématiquement basée à priori sur 2 hypothèses : les faibles pluies s’évaporent entièrement, et « pour des pluviosités très élevées, l’évaporation tend vers zéro, l’air étant sensiblement saturé dans ces conditions », en laissant à un coefficient γ le soin de synthétiser l’influence du climat, du sol et de la végétation. Pour de grands bassins fluviaux, « l’effet propre du terrain et de la végétation est sensiblement constant et la température domine le phénomène » (Hénin et Godard, 1944). Constatant que cette formule sous-estime l’évaporation dans le cas de pluviosités élevées, Turc en 1951 en propose une autre, empirique, prenant en compte la température et basée sur l’hypothèse (qu’il vérifie en 1954) que, lorsque P croît, E tend vers une limite supérieure qui est fonction de la température.
Thornthwaite, 1948 : évapotranspiration potentielle et réelle.
Géographe climatologue, Thornthwaite veut cartographier les climats des USA de la meilleure façon possible. En suivant les travaux de l’Allemand Köppen, il le fait d’abord sur la base de la végétation naturelle, considérée comme intégratrice du climat. Mais cela ne le satisfait pas car non « rationnel », au sens de basé sur des chiffres. Il cherche alors à utiliser la masse de données météo enregistrées. Mais une donnée essentielle n’est pas mesurée : l’évaporation du sol et des couverts végétaux. Peut-on l’estimer à partir des autres ? Il doute d’abord que ce soit possible : « La quantité d’eau enlevée d’un champ par transpiration dépend des besoins en eau des plantes qui y poussent et de leur croissance, qui à son tour peut être limitée par la quantité d’eau disponible. Il s’ensuit que les pertes d’eau depuis les surfaces de terrain, résultant de l’évaporation et de la transpiration, n’ont pas de relation directe aux pertes par évaporation à partir de surfaces d’eau libre. Par conséquent, on ne peut attendre aucune formule empirique donnant des valeurs fiables de l’évaporation et de la transpiration des surfaces de terrain en utilisant les données météorologiques ordinaires » (1942). Il connaît les avancées théoriques de l’époque sur les transferts verticaux dans la basse atmosphère, mais il s’en faut encore de beaucoup pour qu’elles puissent être utilisées en pratique dans ce but.
Il est avant tout pragmatique. Personne n’ayant réussi à séparer de façon satisfaisante l’évaporation depuis la surface du sol et la transpiration des végétaux, il les regroupe en 1948 sous le nom d’évapotranspiration. Ayant constaté empiriquement que celle-ci croît jusqu’à une valeur maximale lorsque les apports d’eau d’irrigation augmentent, il nomme cette valeur maximale évapotranspiration potentielle, (et évapotranspiration réelle celle mesurée dans n’importe quelles conditions).
| « « La combinaison de l'évaporation depuis la surface du sol et de la transpiration des plantes, appelée « évapotranspiration », représente le transport en retour d'eau de la terre vers l'atmosphère, l'inverse des précipitations. (…) La végétation du désert est clairsemée et utilise peu d’eau parce que l’eau manque. Si plus d’eau était disponible, la végétation serait moins clairsemée et utiliserait plus d’eau. Il y a donc une différence entre la quantité d’eau réellement transpirée et évaporée, et celle qui serait transpirée et évaporée si elle était disponible. Quand l’apport d’eau augmente, comme dans un projet d’irrigation dans le désert, l’évapotranspiration s’élève jusqu’à un maximum qui dépend seulement du climat, et que nous pouvons appeler « évapotranspiration potentielle », pour la distinguer de l’évapotranspiration réelle ». » |
Il se résout à estimer cette valeur maximale à partir de la seule température moyenne, qu’il dit plus étroitement corrélée à l’ET que le rayonnement solaire. Mais il reconnaît que « le principal obstacle au développement d’une équation rationnelle est le fait qu’on ne comprend pas pourquoi l’évapotranspiration potentielle correspondant à une température donnée n’est pas la même partout » (1948 : 90-91). S’ensuivent alors des ajustements très laborieux, avec des corrections fonction de la latitude et du mois de l’année, pour produire, à l’échelle du mois, une estimation qui n’est qu’une étape pour calculer des indices d’aridité et d’humidité. La méthode (ou formule) de Thornthwaite n’a pas été créée pour le calcul des besoins de couverts végétaux ou de doses d’irrigation, mais pour une classification géographique des climats, à des échelles de temps (le mois) et d’espace (de l’ordre du dix millionième) éloignées de la pratique agricole.
Malgré les limites exposées par Thornthwaite lui-même et les critiques qui lui ont été faites tôt (Gentili, 1953), sa formule est encore souvent utilisée dans le monde, de façon directe et explicite ou, plus insidieusement, indirecte et implicite, dans la classification climatique de Holdridge[5] (1947, 1967), ou l’indice de sécheresse de Palmer[6]. Son usage est parfois même recommandé, par exemple par le cours numérique Gestion des ressources en eau : des concepts aux territoires de l'action[7], qui affirme qu’elle « a l'avantage d'être robuste sous différentes latitudes », ce qui est faux. Deux exemples : en climat méditerranéen dans le sud de la France, un fort vent de mistral en été fait monter l’ETP de 6 à 9 mm par jour, mais la formule de Thornthwaite indique une baisse à 5 mm/j à cause de la température plus basse (Seguin, 1975). Inversement, derrière un brise-vent qui réduit l'ETP (c’est pour cela qu’on les fait), elle donne un résultat plus élevé puisqu'il fait plus chaud… En haute altitude dans les Andes, elle sous-estime l’ETP de près de moitié, conduisant à des diagnostics climatiques, et donc des politiques agricoles, aberrants (Frère et al., 1974 ; Vacher et al., 1989 ; Morlon & Vacher, 1991).
L’usage de celle de Penman-Monteith est donc infiniment préférable.
Penman, 1948 : formulation physique.
La même année mais de façon indépendante, Penman propose, sur la base d’un bilan d’énergie et de transfert de vapeur, une première formulation théorique, qui fut précisée en 1965 par Monteith (formule de Penman-Monteith[8]) et s’est imposée dans le monde comme la référence pour estimer l’ETP (voir article Évapotranspiration).
Ironie de l’histoire, Penman calibre cette formule en exploitant les données obtenues sur un dispositif expérimental (des lysimètres de 6 pieds de profondeur, contenant les uns de l’eau, d’autres du sol resté nu et d’autres du sol avec du gazon) dont la conception de base était proche de celui installé par La Hire en 1688… Il exprime l’évapotranspiration du gazon et l’évaporation du sol nu comme des fractions de l’évaporation de l’eau libre.
Pendant longtemps, l’usage de la formule de Penman-Monteith fut restreint à ceux qui disposaient de moyens de calculs puissants et aux rares stations météo où les nombreuses données qu’elle exige étaient mesurées, d’où la création d’autres formules - aussi diverses que nombreuses - moins sûres mais d’emploi plus facile. L’avènement de la micro-informatique et des stations météo automatiques en permet maintenant une utilisation beaucoup plus large, rendant les autres sans intérêt.
En France…
L’article de Thornthwaite est présenté en 1950 dans la revue La Météorologie par Curé, qui emploie les expressions d’évapotranspiration potentielle et « actuelle » (anglicisme pour réelle). Mais il a fallu du temps pour que celles-ci soient largement admises dans le domaine agronomique. Bien qu’il y cite Thornthwaite, Turc ne les emploie pas dans sa grosse étude publiée en 1954 et 1955, ni Demolon dans la dernière édition (1956) de Croissance des végétaux cultivés, etc. C’est en 1961 qu’elles sont consacrées dans un numéro des Annales agronomiques de l’INRA faisant suite à une réunion de travail entre bioclimatologues de l’INRA et ingénieurs du Service Hydraulique du Génie Rural.
Après avoir défini l’ETP en référence à Thornthwaite et Penman (voir annexe 6), Turc y expose une méthode de calcul à l’échelle du mois ou de la décade, à partir de données météorologiques standard (température, rayonnement global, humidité relative). Exigeant moins de données et de calculs que celle de Penman, cette méthode a été largement utilisée en France et dans de nombreux pays francophones sous le nom de formule de Turc. A sa suite, Bouchet, comparant (à l’échelle mensuelle) les résultats des formules de Penman (1948), Thornthwaite et Turc, avec des mesures faites sur « évapotranspiromètres » (lysimètres), obtient des « résultats (qui) paraissent assez chaotiques ». En effet, tous les couverts végétaux ne réfléchissent pas la même fraction (albedo) du rayonnement solaire, et, sous un même climat, ne reçoivent donc pas exactement la même quantité d’énergie ; et l’évaporation modifie des facteurs du climat (température et humidité de l’air) qui la déterminent, d’où d’importants effets d’échelle par les transferts latéraux : « ainsi, la mesure de l’ETP n’aura un sens climatique que si l’on prend soin d’éliminer cette action latérale ou « effet d’oasis » parasite à l’échelle où l’on définit le climat. (…) Il en résulte que ETP en tant que facteur climatique n’est accessible à la mesure que sur une échelle d’espace relativement importante, de l’ordre de quelques hectares » (au minimum).
Autres langues
Voir article Évaporation, transpiration végétale, évapotranspiration : les mots.
Notes
- ↑ Après avoir calibré sa formule sur les données de lysimètres, Penman en compare les résultats avec les mesures faites avec d’autres méthodes et à d’autres échelles en divers endroits du monde
- ↑ Hales compare des mesures faites par lui en Angleterre avec celles faites par Cruquius (1724) à l’actuelle frontière entre les Pays-Bas et l’Allemagne... Ce qui importe est d’avoir pris l’évaporation de l’eau libre comme référence.
- ↑ Pas tous cependant ! Parlant de la transpiration des plantes, Boussingault écrit « cette transpiration, on le comprend aisément, est favorisée par la température, la sécheresse et l’agitation de l’air » et « la proportion de vapeur qu'un gaz peut retenir est d'autant plus grande que la température est plus élevée » (1843 : 30 ; 1844 : 691).
- ↑ Au Moyen-âge, Pietro de Crescenzi écrit « Et la finale intencion de la fuelle ((feuille)) est couvrir le fruit et purgier, pource que nature a mestier de purgacion, pour oster la superfluité de l’umeur qui y est. » ([ca. 1306] 1373, livre II, chapitre 6. C’est nous qui soulignons)
- ↑ article de Wikipedia
- ↑ article de Wikipedia
- ↑ Site de l'Université du Mans, consulté le 17 janvier 2017
- ↑ Voir article de Wikipedia ou exposé sur le site de la FAO.)
Références citées
- Bouchet R.J., 1961. Signification et portée agronomique de l’évapotranspiration potentielle. Ann. Agron. INRA, 12 (1) : 51-74.
- Boussingault J.B., 1843-44. Économie rurale considérée dans ses rapports avec la chimie, la physique et la météorologie. Paris, t. 1, 1843, 648 p texte intégral sur Gallica ; t. 2, 1844, 742 p. texte intégral sur Gallica.
- Chouraqui A., 2003. Traduction de la Bible. Desclée de Brouwer, Paris, 2412 p. + annexes.
- Collier D., Robelin M., 1959. Contribution à l’étude de la dynamique de l’eau et des substances chimiques dans les sols argilo-calcaires de Limagne. Résultats de quatre années d’observations lysimétriques. Ann. Agron. INRA, 10 (4) :415.
- Coutagne A., de Martonne E., 1933. De l’eau qui tombe à l’eau qui coule. Évaporation et déficit d’écoulement. Conseil international de recherches, Union géodésique et géophysique internationale, Lisbonne : 97-128.
- Crescens. P. de (Pietro de Crescenzi), [[ca. 1306] 1373] 2023. Le livre des prouffitz champestres et ruraulx de Pierre de Crescens, Vol. 1 : Introduction et texte (livres I-VIII), édité par Fleur Vigneron. Honoré Champion, Paris, 2023, 806 p.
- Cruiziat P., 2007. Comprendre la montée de la sève dans les arbres. De Hales (1727) à Dixon (1914). In : P. Robin, J.P. Aeschlimann, C. Feller (eds), Histoire et agronomie, entre ruptures et durée. IRD, Paris : 203-214.
- Cruquius N., 1724. Observationes accuratae captae... London, Philosophical Transactions for the Months of January and February, 1724: 4-7. texte intégral sur le site de la Royal Society.
- Dalton J., 1802. Experimental essays on the constitution of mixed Gases; on the Force of Steam or Vapour from Water and other Liquids in different temperatures (...); on Evaporation; (...). Memoirs of the Literary and Philophical society of Manchester, 1 (5): 535-602. texte intégral sur Biodiversity Library.
- Dehérain P.P., 1873. Cours de chimie agricole. Paris, Hachette, 616 p. texte intégral sur Gallica.
- Desmarest, 1757. Article « Fontaine ». Encyclopédie, t. 7 : 81-100.
- Dixon H.H., 1914. Transpiration and the ascent of sap in plants. Londres, 217 p.
- Duhamel du Monceau H.L., 1750. Traité de la culture des terres, suivant les Principes de M. Tull, Anglois. Vol. 1, Paris, XXXVI + 488 p. + figures.
- Duhamel du Monceau H.L., 1758. La physique des arbres, t. 2, LXV + 306 p. + planches Paris. texte intégral sur Gallica.
- Frère M., Rijks J.Q., Rea J., 1975. Estudio agroclimatológico de la zona andina. FAO / UNESCO / OMM, Rome, 375 p. + annexes.
- Gasparin A. de, 1860. Cours d’agriculture, t. 6. La Maison rustique, Paris, 614 p.
- Gentili J., 1953. Une critique de la méthode de Thornthwaite pour la classification des climats. Annales de Géographie, 62 (331) : 180-185.
- Guettard J.E., 1748 & 1749. Mémoire sur la transpiration insensible des plantes. Mém. Acad. Royale des Sciences, 1748 : 569-592. Second Mémoire sur la transpiration insensible des plantes. Mém. Acad. Royale des Sciences, 1749 : 265-317. texte intégral sur le site Hatitrust.
- Habault, 1983. Lexique de termes agricoles et horticoles. Termes scientifiques, techniques et économiques. J.B. Baillière, Paris, 1983, 152 p.
- Hales S., 1727. Vegetable Staticks: or, an Account of some Statical Experiments on the Sap in Vegetables, being an Essay towards a Natural History of Vegetation… Londres, 376 p. texte intégral sur le site illustratedgardens.org ; la 3e édition, de 1738, est sur BooksGoogle.
- Hales S., [1727] 1735. La statique des végétaux et l’analyse de l’air. Expériences nouvelles. Traduit par Buffon, Paris, xviii + tables + 408 p.
- Hénin S., Godard M., 1944. Relations entre l’évaporation, la température et l’indice d’aridité. C.R. Acad. Sci., 219 : 559-560
- Hénin S., Ternissien J., 1944. Sur une relation entre la pluviosité, le drainage et l’évaporation. C.R. Acad. Sci., 219 : 80-82
- Holdridge L.R., 1947. Determination of world plant formations from simple climatic data. Science 105 (2727): 367—8.
- Holdridge L.R., 1967. Life zone ecology. Tropical Science Center. San Jose, Costa Rica, 206 p.
- Home F., [1757] 1761. Les principes de l’agriculture et de la végétation. Paris, 155 p (+ 18 p de 2 mémoires d’un auteur français anonyme). texte intégral sur archive.org, ou texte intégral sur openlibrary.org.
- La Hire P., [1703] 1720. Remarques sur l’eau de la pluie, & sur l’origine des Fontaines ; avec quelques particularités sur la construction des Citernes. In : Histoire de l’Académie Royale des Sciences, année 1703, avec les Mémoires de Mathématique & de Physique pour la même année, tirés des Registres de cette Académie. Paris, 1720, 467 p. texte intégral sur Gallica.
- Monteith J.L., 1965. Evaporation and Environment. In: The state and movement of water in living organisms, Symposia of the Society for Experimental Biology, 19: 205-234.
- Morlon P., Vacher J.J., 1991. El frio y la sequedad: dificultades en las evaluaciones climáticas del Altiplano de Perú y Bolivia. In : D. Morales & J.J. Vacher, eds., Actas del VII Congreso Internacional sobre Cultivos Andinos. La Paz, IBTA / ORSTOM / CRDI : 293-296.
- Mühry A., 1860. Allgemeine geographische Meteorologie. 207 p. [1]
- Penman H.L., 1948. Natural evaporation from open water, bare soil and grass. Proc. Roy. Soc. London (A) 193: 120-145.
- Perrault P., 1674. De l’origine des fontaines. Le Petit, Paris, 360 p. Texte intégral (réimpression 1678) sur archive.org ; la partie qui nous intéresse ici sur [hydrologie.org/BIB/perrault/L_origine_des_fontaines.pdf texte intégral] sur le site hydrologie.org.
- Quemada B. (dir), 1983. Trésor de la Langue Française. Dictionnaire de la langue du XIXe et du XXe siècle (1789-1960). CNRS, Paris, t. 10, 1381 p. ]
- Risler E., 1869. Sur l’évaporation du sol. Bibliothèque universelle et Revue Suisse, Archives des sciences physiques et naturelles, Genève, Lausanne, Neuchâtel, t. 36 : 27-33.
- Risler E., 1870. Évaporation du sol et des plantes. 2me mémoire. Bibliothèque universelle et Revue Suisse, Archives des sciences physiques et naturelles, Genève, Lausanne, Neuchâtel, t. 37 : 214-228.
- Risler E., 1871. Recherches sur l’évaporation du sol et des plantes. Troisième mémoire. Bibliothèque universelle et Revue Suisse, Archives des sciences physiques et naturelles, Genève, Lausanne, Paris, t. 42 : 220-263.
- Robelin M., 1962. Évaporation réelle de différents couverts végétaux bien alimentés en eau et évapotranspiration potentielle. Détermination expérimentale. Ann. Agron. INRA, 13 (6) : 493-520
- Rozier F. (abbé), 1783. Article Évaporation. Cours complet d'agriculture... : 408-410. Texte intégral sur Wikisource.
- Sammis T.W., Wang J., Miller D.R., 2011. The Transition of the Blaney-Criddle Formula to the Penman-Monteith Equation in the Western United States. J. of Service climatology, 5 (1): 1-11. texte intégral sur le site stateclimate.org.
- Seguin B., 1975. Étude comparée des méthodes d’estimation d’ETP en climat méditerranéen du sud de la France (région d’Avignon). Ann. agron. INRA, 26 (6) : 671-691.
- Sénebier J., 1791. Physiologie végétale. In : Encyclopédie méthodique, t. 1, viii + 196 p. Paris, Panckoucke. Texte intégral sur Gallica.
- Thornthwaite C.W., 1942. Measurement of Evaporation from Land and Water Surfaces. U.S. Dept. of Agric. Tech. Bull. 817, 143 p. texte intégral su Googlebooks.
- Thornthwaite C.W., 1948. An approach toward a rational classification of climate. Geogr. Rev., 38: 81-86. texte intégral sur Jstor.
- Turc L., 1951. Nouvelle formule pour le calcul du bilan de l’eau en fonction des valeurs annuelles moyennes des précipitations et de la température. C.R. Acad. Sci., 233 : 633-
- Turc L., 1954. Le bilan d’eau des sols: relations entre les précipitations, l’évaporation et l’écoulement. I : l’écoulement annuel moyen des cours d’eau. Ann. Agron. INRA, 5 (4) : 491-595.
- Turc L., 1955. Le bilan d’eau des sols: relations entre les précipitations, l’évaporation et l’écoulement. II : le drainage mensuel des cases lysimétriques. Ann. Agron. INRA, 6 (1) : 5-131.
- Turc L., 1961. Évaluation des besoins en eau d’irrigation, évapotranspiration potentielle. Ann. Agron. INRA, 12 (1) : 13-50.
- Vacher J., Atteia O., Imana E., Choquevilca J., Maldonado R, 1989. Net radiation and Evapotranspiration on the Bolivian Altiplano. 3d Intl. Conf. on Southern Hemisphere Meteorology and Oceanography, Buenos Aires, Amer. Met. Soc., Boston: 169-172.
- Vallemont (Pierre Le Lorrain, abbé de), 1705. Curiositez de la nature et de l’art sur la végétation ou l’Agriculture et le jardinage dans leur perfection… Claude Cellier, Paris, xxxvii + 708 p.
- Vivenot R. von, 1866. Beiträge zur Kenntniss der klimatischan Evaporationskraft und deren Beziehung zu Temperatur, Feuchtigkeit, Luftströmungen und Niederschlägen. Ferdinand Enke Verlag, Erlangen, 104 p. texte intégral.
- Woodward J., 1699. Some Thoughts and Experiments Concerning Vegetation. Phil. Trans., 1699, 21: 193-227.