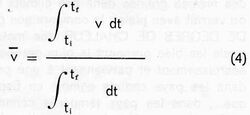Temps thermique (sommes de températures) - Annexe 4

Date de mise en ligne

27 novembre 2023

Retour à l'article

Cette annexe se rapporte à l'article Temps thermique (sommes de températures).

Signification et portée des sommes de températures (Durand, 1969, extraits)

I. HISTORIQUE

(…)
Vers la fin du siècle dernier, une nouvelle idée germa. Pourquoi chercher à assimiler la vitesse de développement à une fonction linéaire de température alors que les plantes sont le siège de réactions chimiques dont la vitesse croît exponentiellement avec la température ? La méthode du Q₁₀ était née : elle consiste à remplacer la somme des températures journalières diminuées d'un seuil par celle d'un coefficient (Q₁₀) fonction exponentielle de la température. Cette méthode se développe rapidement et est encore très utilisée (Bidabe, 1967 ; Niqueux & Arnaud, 1967).

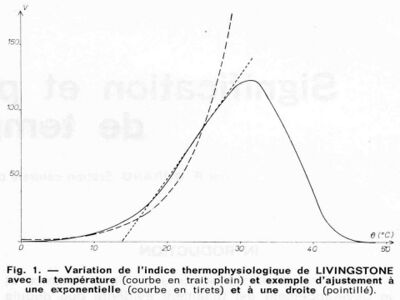
Plus tard, Lehenbauer (1914) étudia la variation de la vitesse de croissance avec la température et les nombreux travaux effectués depuis dans ce sens montrent que la vitesse croît progressivement jusque vers 30° C, puis décroît rapidement jusque vers 36-40° C où elle s’annule, ces températures étant létales. Livingstone (1916), utilisant ces résultats, proposa une nouvelle méthode consistant à faire la somme d'indices proportionnels à la vitesse de croissance : c'est la méthode thermophysiologique.

On se trouve donc en présence de trois méthodes d`évaluation de l'action de la température sur l'évolution des plantes : la méthode des sommes de températures avec seuil d’action, la méthode des sommes de Q₁₀ et la méthode thermophysiologique. Quelle est exactement leur signification et quels sont les avantages et inconvénients respectifs de chacune de ces méthodes ?

II. VITESSE MOYENNE ET VITESSE INSTANTANÉE DE DÉVELOPPEMENT

La courbe (fig. 1) représente l’indice thermophysiologique en fonction de la température, calculé par Livingstone à partir des données de Lehenbauer. Elle donne, dans un système d’unités arbitraires, la vitesse de croissance de plantules de maïs aux diverses températures. On constate par exemple que la vitesse à 25°C (V = 87) est sensiblement le double de celle à 20°C (V = 46). Si l’on maintient la température constante au cours de l’évolution du maïs, le temps nécessaire pour réaliser une phase de développement déterminée sera donc double à 20° C qu’à 25°C (par exemple 22 jours et 11 jours).

Si l’on appelle vitesse de développement V le rapport entre une grandeur arbitraire L et le temps nécessaire à réaliser la phase de développement T, on a la relation :

V = L/T (1)

Dans l’exemple précédent, en prenant L = 1000 et en exprimant le temps en jour, on aura : V = 46 à 20° C et V = 91 à 25° C, soit sensiblement la valeur de l’indice thermophysiologique.

Supposons maintenant que la température varie au cours de la phase considérée. A chaque instant, nous aurons une température G, à laquelle correspondra une vitesse V. On peut admettre que pendant le court intervalle de temps dt, la température et, par conséquent la vitesse, restent constantes; le développement progresse d'une petite quantité dl. On peut alors écrire que :

V = dl/dt (2)

La réalisation complète du développement L est égale à la somme des développements élémentaires dl. On peut donc écrire :

où ti et tf représentent les instants initial et final de la phase. La relation (1) est toujours valable, V représente alors la vitesse moyenne de développement au cours de la phase considérée puisque, par définition, la valeur moyenne V de v pendant l’intervalle de temps T = tf – ti est :

On en déduit que :

v peut alors être considéré comme une vitesse instantanée de développement à l’instant t ; elle n’est pas accessible à la mesure, comme sur un compteur de voiture, mais existe réellement. Les mesures d’accroissement, au cours de la phase considérée, à intervalle de temps relativement grand (la journée par exemple), donnent une idée de cette vitesse instantanée de développement mais elles doivent être corrigées, la croissance n'étant pas proportionnelle au temps.

Le problème de la liaison entre le développement et la température réside donc dans l’intégration de la relation (3). La vitesse v est fonction de la température Θ, elle-même fonction du temps t. Théoriquement l’intégration est donc possible ; mais la relation v = f (Θ) représentée graphiquement (fig. 1) n’a pas une expression mathématique simple et la relation Θ = g(t) prend également des formes très variées, impossible à traduire mathématiquement, dans les conditions naturelles. L’intégration ne peut donc se faire par le calcul ; on doit avoir recours à des approximations. On a vu que trois méthodes sont habituellement utilisées, examinons-les en détail.

III. DÉTERMINATION DES VITESSES MOYENNES DE DÉVELOPPEMENT

(…)

d) Mode de calcul des sommes de températures et des sommes de Q₁₀

On n’insistera pas sur la méthode thermophysiologique qui ne présente pas de difficulté théorique d'application. Bien que théoriquement la plus précise, elle fut très peu employée pour deux raisons principales ; la première tient à la lourdeur des calculs : dépouillement horaire des températures, recherche de l'indice thermophysiologique et sommation de ces indices. L'utilisation de calculateurs électroniques devrait permettre d'alléger ces calculs fastidieux. La seconde est plus grave : on connait très mal la courbe d’action de la température sur la vitesse de développement ; on verra d’ailleurs plus loin qu’elle n'a pas le sens absolu qu’on lui prête.

Les méthodes des sommes de températures ou de coefficients de température ne nécessitent pas la connaissance de cette loi d’action. Les paramètres (seuil apparent de développement et valeur de la somme pour les sommes de température ; valeur du Q₁₀ et des sommes de coefficients par la méthode du Q₁₀) sont déterminés expérimentalement par des méthodes statistiques plus ou moins élaborées.

La majorité des auteurs procèdent de la façon suivante : on collecte les observations phénologiques sur une phase de développement donnée plusieurs années de suite. On effectue ensuite, pour chaque année, la somme des températures moyennes journalières avec différents seuils ou la somme des coefficients de températures pour diverses valeurs de Q₁₀. Dans le cas des sommes de températures, on élimine les journées pour lesquelles la température moyenne est inférieure au seuil. On recherche ensuite la valeur moyenne et l'écart type de ces diverses sommes pour l'ensemble des années (une dizaine d’années semble un minimum pour faire une telle étude). Le choix du meilleur système se fait soit en prenant celui pour lequel le coefficient de variation (rapport écart-type/Moyenne) est le plus faible, soit celui pour lequel l`écart-type, exprimé en jours moyens, est le plus faible. Pour exprimer l'écart-type en jours moyens, on détermine la température moyenne au cours de la phase considérée pour l'ensemble des années; on calcule ensuite le coefficient qu'apporte cette journée et on divise l'écart-type par cette valeur. Supposons par exemple que l`on arrive à une somme de 500 degrés-jours et un écart-type de 14 degrés jours dans un système de sommation de température avec seuil de 5°C, la température moyenne au cours de la phase étant de 12°C. Un jour moyen apporte une contribution à la somme de températures de 12°–5° = 7 degrés jours. L'écart-type, exprimé en jours moyens est alors égal à 14/7 = 2 jours moyens. Ce qui veut dire que, dans 98 % des cas, la somme des températures donnera la durée de la phase à ± 4 jours (deux fois l'écart-type).

L’emploi des calculateurs permet des méthodes plus élaborées de recherches. Citons par exemple le travail de Bassett et al. (1961) qui effectue une série de régressions linéaires pour déterminer le seuil apparent de développement : une première régression, avec un seuil très bas, permet une première estimation du seuil; un nouveau calcul est effectué avec ce seuil, les journées où la température est inférieure à ce seuil étant éliminées ; le processus est renouvelé jusqu'à ce que les interventions suivantes n'apportent plus de modification.

On pourrait de la même façon faire un ajustement statistique à une fonction exponentielle pour en déterminer les paramètres ; mais d'autres fonctions (un développement polynomial par exemple) pourraient s'ajuster encore mieux aux courbes expérimentales.

Les variantes de ces méthodes sont très nombreuses : certains auteurs utilisent uniquement les températures maximales ou minimales, ou encore les deux au lieu de la température moyenne ; d'autres utilisent un seuil pour les températures élevées, etc. Nous n’entrerons pas dans le détail de ces divers procédés.

Parfois, on ne connait pas le début de la phase de développement considéré, tel est le cas lorsque l'on veut relier à la température la date de floraison d'arbres présentant au cours de l’hiver un repos végétatif. Le problème est résolu soit en prenant une date fixe (généralement le 1er octobre, le 1er janvier ou le 1er mars suivant les régions (Bassett et al., 1961), soit en calculant les sommes de développement à partir de diverses dates initiales et en cherchant celle pour laquelle le coefficient de variation d’une année à l'autre est le plus faible (Bidabe, 1967) ; cette dernière méthode donne généralement la mi-janvier comme date la plus favorable.

Références :

• Durand R., 1969. Signification et portée des sommes de températures. Bull. Tech. Inf. 238, 1969. Météorologie et agriculture, vol. 2 : 185-190.
• Bassett I.J., Holmes R.M., Mackay K.H., 1961. Phenology of several plant species at Ottawa, Otario and an examination of the influence of air temperatures. Canad. J. Plant Sci., 41 : 643-652. Texte intégral
• Bidabe B., 1967. Action de la température sur l’évolution des bourgeons de pommier et comparaison de méthodes de contrôle de l’époque de floraison. Ann. Physiol. Vég., 9 (1) : 65-86.
• Lehenbauer P.A, 1914. Growth of maize seedlings in relation to temperature. Physiol. Res., 1 (5): 247-288. Texte intégral
• Livingstone B.E., 1916. Physiological temperatures indices for the study of plant growth in relation to Climatic conditions. Physiol. Res. 1.8 : 399-420.
• Niqueux M., Arnaud H., 1967. Recherche d'une relation entre précocité d’épiaison et températures pour quelques variétés de graminées fourragères observées en France. Ann. Physiol. veg., 9 (1) : 29-64.