Drainage - Annexe 2
| Cette annexe se rapporte à l'article Drainage. |
Fonctionnement du réseau et tranchée de drainage
Approche hydraulique et modélisation des débits
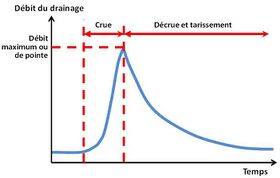
L’hydrogramme qui traduit la réponse dans le temps du réseau à un épisode pluvieux, se compose généralement de 3 phases successives en régime non influencé (fig. 1):
- A : augmentation du débit (crue) ;
- B : débit maximum ou débit de pointe ;
- C : diminution puis arrêt du débit (décrue et tarissement).
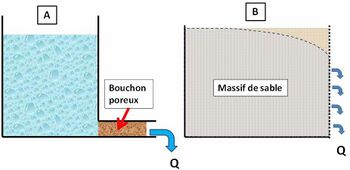
La phase de décroissance du débit (phase C) s’analyse au moyen de modèles d’écoulement (Roche, 1963 : 267) :
- vidange d’un bac à travers un bouchon poreux, représenté par une loi exponentielle :
- vidange d’un bac de sable saturé à travers une paroi perforée :
Les 2 paramètres α et β sont proportionnels au coefficient de perméabilité K des massifs poreux (fig. 2).
Alors que Roche utilise ces lois pour l’analyse du tarissement d’un cours d’eau, Boussinesq décrit ainsi le tarissement de sources drainant un aquifère selon qu’elles se situent nettement au dessus du niveau imperméable ou reposent sur ce dernier (Lessafre, 1987).
Les meilleurs ajustements d’hydrogrammes enregistrés s’obtiennent selon les cas sur l’une ou l’autre loi (Lessafre, 1987 ; Kosuth & Lessafre ; 1984), parfois un même épisode de drainage peut être divisé en plusieurs phases successives suivant la même loi (Alessandrello et al., 1976) ou des lois différentes (Trouche, 1981d). Ceci montre bien la complexité de l’écoulement de l’eau dans un sol drainé, chaque couche du profil ayant sa propre dynamique hydrique et l’hydrogramme enregistré en sortie du réseau en est la résultante.
Évolution saisonnière des écoulements de drainage
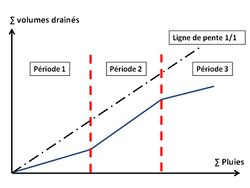
Le rapport Quantité d’eau drainée/Précipitation qui est le rendement hydraulique du réseau, dit « coefficient de restitution », varie au cours d’une même saison de drainage. Le graphique en double cumul des pluies et des volumes drainés met en évidence 3 périodes successives (fig 3) (Kosuth & Lessafre, 1984) :
- 1 - période d’amorce du drainage : en début de saison le sol est sec, les précipitations remplissent progressivement la réserve en eau du sol, le débit de drainage est inférieur aux précipitations, le coefficient de restitution est très faible (10 à 20%) puis augmente progressivement ;
- 2 - période de drainage intense : le sol est saturé, l’eau reçue s’écoule dans les drains, le coefficient de restitution est alors proche de 100% ;
- 3 - période de tarissement : les pertes par évapotranspiration sont supérieures aux apports des pluies, la réserve en eau se vide progressivement et le sol se désature, le coefficient de restitution diminue progressivement jusqu’à l’arrêt du drainage.
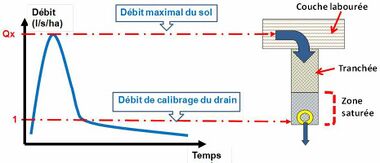
Les valeurs de débit de pointe de 3 à 5 l/s/ha ont été plusieurs fois enregistrées sur des dispositifs expérimentaux non limitatifs en débit (Guyon, 1972a ; Trouche, 1981e ; Kosuth & Lesaffre, 1984). Elles dépassent la valeur de 1 l/s/ha très souvent retenue dans la pratique pour le calcul des projets de drainage. Dans ce cas, la tranchée de drainage joue le rôle de réservoir tampon entre l’eau provenant de la nappe perchée dans la partie supérieure du sol (débit 3 à 5 l/s/ha) et le drain (débit 1 l/s/ha). Des périodes de stagnation d’eau plus ou moins longues se produisent en fond de tranchée jusqu’à la vidange complète de celle-ci (Trouche, 1991). Ce phénomène accroît le risque de détérioration du sol autour et au dessus du drain. (fig. 4).
Évolution des tranchées de drainage
L’altération du fonctionnement de la tranchée conditionne la durée de vie du réseau. Les observations de tranchées de réseaux de drainage d’âges divers indiquent que le facteur temps ne peut à lui seul expliquer la dégradation progressive de l’état structural de la tranchée (Trouche, 1981 b & e).
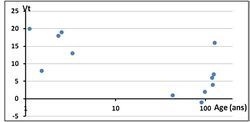
L’état de la tranchée de drainage est évalué par un indice de vieillissement :
calculé à partir des mesures de la densité apparente sèche du sol dans l’interdrain (di) et dans la tranchée (dt) à un niveau situé sous la profondeur du labour. Il est d’autant plus élevé que la tranchée est en bon état. Les valeurs obtenues correspondent bien à la qualité de fonctionnement du réseau observée sur le terrain. La figure 5 montre que globalement la valeur de l’indice Vt, donc la qualité de l’effet tranchée, décroit avec l’âge du réseau, mais pour certains d’entre eux, bien que plus que séculaires au moment des mesures, les valeurs sont comparables à celles des réseaux plus récents.
En effet, le matériau sol mémorise une partie des contraintes subies au cours de son histoire, phénomène bien connu des mécaniciens du sol sous le nom de « pression de pré-consolidation ». Ces contraintes sont naturelles au cours de la pédogénèse, ou d’origine anthropique liées par exemple au roulage d’engins ou au passage d’outils. Il en résulte une limitation au gonflement plus ou moins importante lors des phases d’humectation. Soumis à des phases de dessèchement et de réhumectation, les matériaux argileux montrent, à des degrés divers selon leur nature minéralogique, une certaine irréversibilité des phénomènes retrait-gonflement (Tessier 1984 a,b). Dès lors, des matériaux ayant mémorisé des niveaux élevés de contrainte ont une bonne aptitude à assurer la tenue de l’effet tranchée. Le dessèchement à l’air libre, avant rebouchage, du matériau excavé au creusement de la tranchée va dans le même sens (de Crécy, 1981).
Certains sols à structure instable mis en remblai de la tranchée ne peuvent garantir le maintien à long terme de la capacité filtrante de celle-ci. L’utilisation du gravier en remplacement de la terre d’origine entraîne un surcoût important qui conduit alors à étudier avec attention le volet économique du projet.
Références citées
- Alessandrello E., Concaret J., Guyot J., Perrey C., 1976. Circulation de l’eau en sols limoneux lessivés hydromorphes drainés. C.R. Acad. Agric. Fr., 62 (5) : 364-373. Texte intégral sur Gallica.
- Boussinesq J. 1877. Essai sur la théorie des eaux courantes. Mémoire présenté à l’Académie des Sciences de l’Institut de France. 23, 1-680.
- Boussinesq J. 1904. Recherches théoriques sur l'écoulement des nappes d'eau infiltrées dans le sol et sur le débit des sources. Journal de mathématiques pures et appliquées, 10, 1,5-78 et 10, 4, 363-394
- Crécy J. de, 1981. Dynamique structurale et histoire du matériau. In : Concaret J., dir., Le drainage agricole. Théorie et pratique. Chambre d’Agriculture de Bourgogne : 163-180.
- Guyon G., 1972. Expérimentation sur le drainage entreprise par le C.T.G.R.E.F. à Antony. Bull. Techn. Inf., 273-274 : 921-946.
- Kozuth P., Lesaffre B., 1984. Huit ans d’expérimentation sur trois réseaux de drainage en sols à excès d’eau temporaire. Méthode d’analyse des données et applications. . In : C.R. colloque Fonctionnement hydrique et comportement des sols, AFES, Dijon, 229-250.
- Lesaffre B., 1987. Recherches théoriques et expérimentales sur le fonctionnement du drainage. Essai de synthèse des travaux français. C.R. Acad Agric. Fr., 73 (4), 11-21. [ Texte intégral] sur Gallica.
- Roche M. 1963. Hydrologie de surface. ORSTOM & Gauthier-Villars, Paris, 429 p.
- Tessier D., 1984a. Comportement hydrique des matériaux argileux en relation avec leur organisation. Conséquences sur les propriétés macroscopiques. In : C.R. colloque AFES, Fonctionnement hydrique et comportement mécanique des sols, Dijon : 297-308.
- Tessier D., 1984b. Étude expérimentale de l’organisation des matériaux argileux. Hydratation, gonflement et structuration au cours de la dessiccation et de la réhumectation. Thèse Dr. État, univ. Paris VII, 361 p.
- Trouche G. 1981a. Aspects agronomiques et hydrodynamiques du drainage des sols à profil différencié du val de Saône. Thèse Doct-Ing., Univ. Dijon, 201 p.
- Trouche G., 1981b . Permanence de l’effet tranchée. In : Concaret J. (dir), Le drainage agricole. Théorie et pratique. Chambre d’Agriculture de Bourgogne, 15, 215-228.
- Trouche G., 1991. Étude in situ de la mise en charge des tranchées de drainage. Premières observations à Virey (71). In : Favrot J.C., Penel M. (coord), Le fonctionnement du drainage : approche pédo-hydraulique. Ét. Hydraulique agricole, Cemagref, 10 : 121-138.